
 |
 |
The chapter culminates with a script that automatically identifies 12-tone row variants in complex orchestral scores. The general approach is instructive for applications beyond serial analysis.
In set theoretic applications it is common to use pitch-class
representations.
The
pc
command can be used to transform pitch-related representations
(such as
**pitch,
**freq
and
**kern)
to a conventional pitch-class
notation where pitch-class C is represented by the value zero.
With the
-a
option,
pc
will generate outputs where the pc values `10' and `11' are
rendered by the alphabetic characters `A' and `B' respectively.
Using the alpha-numeric pc representation is recommended;
it proves to be especially convenient for searching tasks since,
otherwise, the characters 1 and 0 do not uniquely specify a single pitch-class type.
A common set theoretic task is identifying occurrences of various
pitch-class set forms.
Figure 34.1 identifies the set forms for several sample vertical sonorities.
These forms are identified using standard numerical designations
(see Forte, 1973; Rahn, 1980).
Set forms are insensitive to transposition, pitch-inversion, and pitch spelling
so all major and minor triads
are identified as pitch-class set 3-11.
Similarly, the dominant seventh chord and `Tristan' chord are similarly related
by inversion so both are identified as pc set 4-27.
Figure 34.1. Examples of PC set forms.
The pcset command identifies pitch-class sets from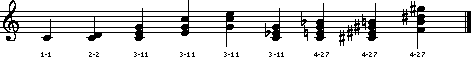
**pc
or
**semits
input.
Illustrated below are the corresponding
**kern,
**pc
and
**pcset
representations
for Example 34.1.
**kern**pc**pcset4c01-14c 4d0 22-24c 4e 4g0 4 73-114e 4g 4cc4 7 03-114g 4cc 4ee7 0 43-114c 4e- 4g0 3 73-114c 4e 4g 4b-0 4 7 104-274c# 4e# 4g# 4b1 5 8 114-274f 4b 4dd# 4gg#5 11 3 84-27*-*-*-
Suppose we wanted to identify the pc sets for successive vertical sonorities in the first movement of Webern's Opus 24 concerto. First, we translate the input to a pitch-class representation, and then we apply the pcset command:
pc opus24 | pcset
Of course this command will only identify the set forms for pitches that have concurrent attacks. If any pitch is sustained, pcset won't know that some null tokens indicate sustained pitch activity. We can rectify this by using the ditto command (Chapter 15) to fill-out the null tokens:
pc opus24 | ditto -s ^= | pcset
If we wanted, we could assemble the resulting
**pcset
spine to the original input.
This would allow us to search for particular patterns that
are coordinated with certain pitch-class sets.
For example, we might be interested in comparing the pitch-class
sets that coincide with the beginnings of slurs/phrases
versus those pitch-class sets coinciding with the ends of slurs/phrases.
First we generate the **pcset spine:
pc opus24 | ditto -s ^= | pcset > opus24.pcs
Then we assemble this spine to the original input score:
assemble opus24 opus24.pcs > opus24.all
Now we can search for data records containing phrase (`{}') or slur ('()')
markers.
Using
yank
-m ... -r 0
rather than
grep
assures that the output retains the Humdrum syntax (see
Chapter 12).
Maintaining the Humdrum syntax will allow us to use
extract
to isolate just the **pcset data.
Finally, we create an inventory of the pc sets.
The process is repeated -- once for beginning slurs/phrases, and
once for ends of slurs/phrases.
yank -m '[{(]' -r 0 opus24.all | extract -i '**pcset' \
| rid -GLId | sort | uniq -c
yank -m '[)}]' -r 0 opus24.all | extract -i '**pcset' \
| rid -GLId | sort | uniq -c
Two pitch-class set inventories will be generated: one inventory for the beginnings of phrases/slurs and one for phrase/slur endings.
Incidentally, the pcset command supports a -c option that can be used to generate the set complement rather than the principal set form.
The 3-11 set form designates both the major and minor chords (since they are symmetrical). In order to distinguish symmetrical forms, it is sometimes useful to represent pitch-class sets using either prime form (the pf command) or normal form (the nf command).
Suppose we wanted to count the proportion of phrase endings in music by Alban Berg where the phrase ends on either a major or minor chord. First, we locate all works composed by Berg:
BERG=`find /scores -type f -exec grep -l '!!!COM.*Berg,' "{}" ";"`
Let's put all the Berg works in a single temporary file:
cat $BERG > AllBerg
Next we generate the normal set forms:
pc AllBerg | ditto -s ^= | nf > AllBerg.nf
Assemble the
**nf
spine with the original scores:
assemble AllBerg AllBerg.nf > AllBerg.all
Now we're ready to count the number of phrases that match the appropriate patterns. First, count the total number of phrases:
grep -c '}' AllBerg.all
Count the number of phrases that end with a major chord:
grep -c '}.*\t(047)' AllBerg.all
And count the number of phrases that end with a minor chord:
grep -c '}.*\t(037)' AllBerg.all
Interval vectors identify the frequency of occurrence of various
interval-classes for a given pitch-class set.
The
iv
command generates the six-element interval vector for any of several
types of inputs -- including semitones
(**semits),
pitch-class
(**pc),
normal form
(**nf),
prime form
(**pf),
and pitch-class set
(**pcset).
The following example shows several different pitch-class sets,
their corresponding pitch-class sets and (right-most spine), the
associated interval vector.
**pc**pcset**name**iv 01-1tone<000000>0 22-2major second<010000> 0 3 73-11minor triad<001110> 0 4 73-11major triad<001110> 0 4 7 104-27dominant seventh<012111> 1 5 8 114-27dominant seventh<012111> *- *- *-*-
Suppose we wanted to determine whether Arnold Schoenberg tended to use simultaneities that have more semitone (interval-class 1) relations and fewer tritone (interval-class 6) relations. As before, we might translate his scores to pitch-class notation, fill-out the sonorities using ditto, and then determine the associated interval vectors for each sonority. Interval vectors without semitone relations will have a zero in the first vector position (i.e., <0.....>) whereas interval vectors without tritone relations will have a zero in the last position (i.e., <.....0>).
pc schoenberg* | ditto -s ^= | iv | grep -c '<0.....>'
pc schoenberg* | ditto -s ^= | iv | grep -c '<.....0>'
So far, we have processed only "vertical" sets of concurrent pitches. In set-theory analyses, there are many other important ways of "segmenting" the musical pitches into pitch-class sets. As we saw in Chapter 19, the context command provides a useful way of grouping together successive data tokens.
Suppose, for example, we wanted to analyze set forms in Claude Debussy's
Syrinx
for solo flute.
The opening measures are shown in Example 34.1.
Example 34.1. From Claude Debussy, Syrinx for flute.
There are a number of ways we might want to try segmenting the melodic line. One possibility is to regard slurs or phrases as indicating appropriate groups. Recall that the -b and -e options for context are used to specify regular expressions that match the beginning and end (respectively) of the context group: We can invoke an appropriate context command, translate the output to a pitch-class representation, and then use the pcset command to identify the set names:
context -b '[{(]' -e '[})]' syrinx | pc | pcset
Perhaps we might consider gathering groups of three successive notes together, and then generating an inventory of the set forms associated with such a segmentation:
context -n 3 -o '[=r]' syrinx | pc | pcset | rid -GLId \
| sort | uniq -c
Another possibility is to treat rests as segmentation boundaries.
context -e r syrinx | pc | pcset
When a work consists of more than one instrument or part,
useful segmentations can be made by extracting each instrument
individually, using
context
to generate musically-pertinent sets, and then assembling all
of the
**pcset
spines into a single file.
Twelve-tone music raises additional analysis issues. Variants of a tone-row can be generated using the reihe command. Given some input, reihe will output a user-specified transformation. Options are provided for prime transpositions (-P option), for inversions (-I option), for retrogrades (-R option) and for retrograde-inversions (-RI option).
Inputs do not have to be 12-tone rows. The 5-tone row used in Igor Stravinsky's "Dirge-Canons" from In Memoriam Dylan Thomas is as follows:
**pc23654*-
The following command will generate a prime transposition of the tone-row so that it begins on pitch-class 6:
reihe -P 6 memoriam
The result is:
**pc671098*-
Generating the inversion beginning at pitch-class 2 would be carried out using the following command.
reihe -a -I 2 memoriam
The -a option causes the values `10' and `11' to be rendered alphabetically as `A' and `B'.
The reihe command also provides a shift operation (-S) that is useful for shifting the serial order of data tokens forward or backward. Consider the following command:
reihe -S -1 memoriam
This shifts all of the data tokens back one position so the data begins with the second value in the input, and the first value is moved to the end:
**pc36542*-
The shift option for reihe can be used to shift any type of data -- not just pitches of pitch-classes. For example, one might use the shift option to rotationally permute dynamic markings, text, durations, articulation marks, or any other type of Humdrum data. In Chapter 38 we will see how the shift option for reihe can be effectively used in many applications apart from serial analysis.
The first step in automated row-finding is to generate a
set matrix of all the set variants.
Typically, the user begins with a hypothesized tone row.
Suppose the tone-row was stored in a file called
primerow.
From this we can generate the entire set matrix.
There is a Humdrum
matrix
command that automatically generates a set matrix,
but let's create our own script to see how this can be done.
The following script uses the
reihe
command to generate each set form.
Each form is stored in a separate file with names such
as I8 and RI3.
There are two noteworthy features to this script.
Notice that the alphanumeric system (-a option) is used
-- so the values `A' and `B' are used rather than `10' and `11';
this will facilitate searching.
Also notice that our script provides an option that allows us to specify
partial
rows:
that is, we can store (say) only the first 5 notes in each tone
row file.
This feature will also prove useful when doing an automatic search.
###################################################################
# MATRIX
# This script generates a tone-row matrix for a specified prime row.
# The -n option is used to specify the number of pitches to be out-
# put in each row-file (e.g. the first 7 pitches of a 12-tone row).
#
# Usage: matrix -n N primerowfile
#
if [ "x$1" != "x-n" ]
then
echo "-n option must be specified."
echo "USAGE: matrix -n number primerowfile"
exit
fi
if [ ! -f $3 ]
then
echo "File $3 not found."
echo "USAGE: matrix -n number row-file"
exit
fi
# Generate the primes, inversions, retrograde, etc:
X=0
while [ $X -ne 12 ]
do
reihe -a -P $X $3 | rid -GLId | head -$2 > P$X
reihe -a -I $X $3 | rid -GLId | head -$2 > I$X
reihe -a -R $X $3 | rid -GLId | head -$2 > R$X
reihe -a -RI $X $3 | rid -GLId | head -$2 > RI$X
let X=$X+1
done
For any given input, the above script produces 48 short files named P0, P1, ... I0, I1 ... R0, R1 ... RI10, RI11.
Each of the row variant files can be used as a template for the patt command (see Chapter 21). The following "rowfind" script shows how the Humdrum tools can be coordinated to carry out an automatic search and identification of tone row variants for some score.
The first part of the script simply checks to ensure that all of the row variant files are present:
###################################################################
# ROWFIND
#
# This script carries a preliminary tone-row search in a specified
# score. It assumes that a complete set of set-variant files exists
# in the current directory, named P0-P11, I0-I11, R0-R11, and RI0-RI11.
#
# This script puts a file named "analysis" which may be assembled
# with the original input file.
#
# Invoke:
# rowfind scorefile
#
# Check that the specified input file exists:
if [ ! -f $1 ]
then
echo "rowfind: ERROR: Input score file $1 not found."
exit
fi
# Also check that the row-variant files exist:
X=11
while [ $X -ne -1 ]
do
if [ ! -f P$X ]
then
echo "rowfind: ERROR: Row file P$X not found."
exit
fi
if [ ! -f I$X ]
then
echo "rowfind: ERROR: Row file I$X not found."
exit
fi
if [ ! -f R$X ]
then
echo "rowfind: ERROR: Row file R$X not found."
exit
fi
if [ ! -f RI$X ]
then
echo "rowfind: ERROR: Row file RI$X not found."
exit
fi
let X=$X-1
done
The following two lines of the script prepare the input score for searching. Specifically, the score is transformed to pitch-class notation (using pc) and then all rests are changed to null tokens using the humsed command. Notice the use of the -a option for pc in order to use the alpha-numeric pitch-class representation.
pc -at $1 > temp.pc
humsed 's/r/./g' temp.pc > score.tmp
The main searching task is done by patt.
The
patt
command is executed 48 times -- once for each row variant.
The
-t
(tag) option is used so that a **patt output is generated.
Each time a match is made the appropriate name (e.g. P4) is output in the spine.
The
-s
option is used to skip barlines and null data records when matching patterns.
The
-m
option invokes the multi-record matching mode -- which allows
patt
to recognize row statements where several nominally successive pitches
are collapsed into a vertical chord:
# Search for instances of each tone-row variant.
X=0
while [ $X -ne 12 ]
do
patt -s '=|^\.(\t\.)*$' -f P$X -m score.tmp -t P$X \
| extract -i '**patt' > P$X.pat
patt -s '=|^\.(\t\.)*$' -f I$X -m score.tmp -t I$X \
| extract -i '**patt' > I$X.pat
patt -s '=|^\.(\t\.)*$' -f R$X -m score.tmp -t R$X \
| extract -i '**patt' > R$X.pat
patt -s '=|^\.(\t\.)*$' -f RI$X -m score.tmp -t RI$X \
| extract -i '**patt' > RI$X.pat
let X=$X+1
done
Each of the above 48
patt
searches resulted in a separate temporary output file.
It would be convenient to reduce all 48 **patt spines into a single
aggregate spine.
This can be done using the
assemble
and
cleave
commands:
# Now we have a lot of files to assemble:
assemble P*.pat > prime.pat
cleave -d ' ' -i '**patt' -o '**rows' prime.pat > analysis.1
assemble I*.pat > inversion.pat
cleave -d ' ' -i '**patt' -o '**rows' inversion.pat > analysis.2
assemble R*.pat > retro.pat
cleave -d ' ' -i '**patt' -o '**rows' retro.pat > analysis.3
assemble RI*.pat > retroinv.pat
cleave -d ' ' -i '**patt' -o '**rows' retroinv.pat > analysis.4
assemble analysis.[1-4] > temp
cleave -d ' ' -i '**rows' -o '**rows' temp > analysis.out
# Finally, clean up some temporary files:
rm [PRI][0-9].pat [PRI]1[01].pat RI[0-9]*.pat temp.pat
rm analysis.[1-4] temp temp.pc score.tmp
There are a few subtleties and problems that deserve mention about our rowfind script. In general, shorter patterns are easier to find than longer patterns. Since row statements tend to be unique after the first 4 or 5 notes, it is preferable to clip the row patterns used as templates. Reducing the length of the templates can lead to "false hits" -- but these tend to be infrequent and are easily recognized.
Applied to an entire multi-part score, rowfind may miss concurrent row statements due to interposed notes appearing in an irrelevant instrument or part. This problem can be avoided by first extracting individual parts and running rowfind on each part separately. (The results can then be amalgamated using assemble and cleave.) On the other hand, searching instruments separately can mean that row statements crossing between instruments may be missed. This problem can be addressed by extracting pairs and groups of instruments and analyzing them together.
For a complex work like Webern's Opus 24 Concerto, this strategy of analyzing both individual instruments and groups of instruments works very well.
In this chapter we have discussed several tools related to set theory analysis. These include the pc (pitch-class) command, the pcset command (for identifying set-forms), and the reihe command (for generating set variants).
We have seen how general tools like context can be used to carry out segmentation of some score. Similarly, we have seen how the patt command can be used to identify tone-row statements.
Two scripts were described in this chapter: matrix and rowfind. These demonstrated how the tools may be coordinated to carry out various automated processes.
This chapter has only scratched the surface regarding the types of pertinent serial-related manipulations that might be pursued. For example, much more sophisticated approaches to segmentation can be created by using some of the layer techniques described in the next Chapter. Similarly, the pattern searches could easily be expanded to look at other parameters typical of "complete serialism" -- such as durations, dynamics, articulation marks, and so on.